Учебное пособие 1817

8.2. Плотность распределения времени безотказной работы элемента на участке (t1 ,t2 ) постоянна и равна нулю вне этого участка (рис. 1.15). Найти интенсивность отказов и построить график.

Рис. 1.15

Решение. Интенсивность отказов по формуле (7) равна

График интенсивности отказов приведен на рис. 1.16.

141

Рис. 1.16

8.3. Простая система состоит из 7 независимых элементов, надежность каждого из которыхp = 0,9 .Найти надежность системы.

Решение. Воспользуемся формулой (10), тогда

P = 0,97 » 0,478.

8.4. Простая система состоит из 100 одинаково надежных независимых элементов. Какова должна быть надежность отдельного элемента, чтобы надежность системы была бы не менее 0,85?

Решение. Представим формулу (10) в виде p = n P . Тогда надежность отдельного элемента

Отсюда надежность элементов

Интенсивность отказа каждого элемента по формуле (7) равна

Интенсивность отказов системы находим по формуле (11)

= 2(1 - t + 2t 2 - 2t 3 + 3t 4 ) . (1 - t 3 )(1 - t + t 2 )

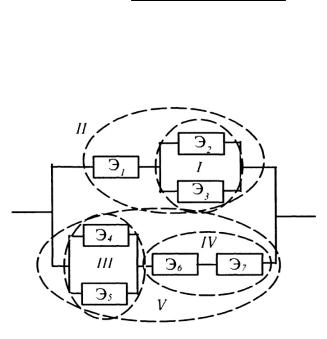
8.6. Найти надежность системы, состоящей из семи элементов с надежностями p1 , p2 ,..., p7 (рис. 1.17).

Рис 1.17

Решение. Поскольку в системе применяются как «последовательное», так и «параллельное» соединение элементов, то при оценке надежности расчленяем ее на ряд подсистем. Рассматривая подсистемы как условные элементы, находим надежность системы в целом.

Подсистема I — «параллельно» включенные элементы Э2 и Э3 ; надежность p1 = 1 - (1 - p2 )(1 - p3 ).

работает, то первый индекс равен нулю, если основная машина отказала, то первый индекс равен единице, а второй индекс определяет число исправных резервных машин. Так, S0k , —

основная машина исправна, из резервных исправны k машин ( k =О, 1, 2, 3); S1k — основная машина отказала, из резервных исправны k машин, причем одна из них работает.

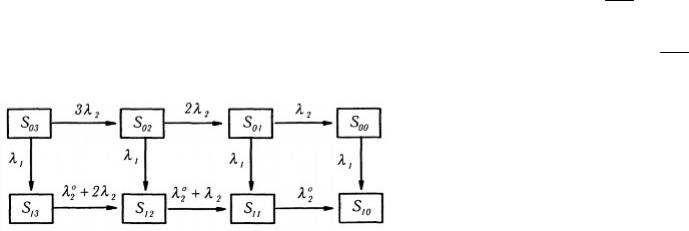
Для составления уравнений Колмогорова представим граф состояний (рис. 1.18).

Рис. 1.18

Система уравнений вероятностей состояний в этом случае будет

dp11 = -l2 0 p11 + l1 p01 + (l2 0 + l2 ) p12 ;

dt

dp10 = l1 p00 + l2 0 p11 .

dt

Из интегрирования первого уравнения системы имеем

p03 = e -(l1 +3l2 )t .

Подставляя это решение во второе уравнение системы и интегрируя, находим p02 .Продолжая последовательно процесс интегрирования уравнений, находим остальные значения вероятностей состояний. Вероятность состояния, когда линия не работает, может быть найдена из условия

p10 (t) = 1 - ( p03 + p02 + p01 + p00 + p13 + p12 + p11 ).

Отсюда надежность линии, как обратное событие, будет

P(t) = 1 - p10 (t).

т. е. равна сумме вероятностей, при которых линия работает. Нетрудно заметить, что изменение числа резервных машин

в технологической линии приводит только к увеличению или уменьшению графа состояний (рис. 1.18), а, соответственно, и числа уравнений системы. В остальном схема расчета остается без изменений.

146

III.Решение задач оптимизации

всистеме МатLав

1.Пакет оптимизации Optimization Toolbox

1.1.Назначение и возможности пакета

Пакет оптимизации(Optimization Toolbox) — это библиотека функций, расширяющих возможности системы МАТLАВ по численным вычислениям и предназначенная для решения задач оптимизации систем нелинейных уравнений. Поддерживает основные методы оптимизации функций ряда переменных:

•Безусловная оптимизация нелинейных функций.

•Метод наименьших квадратов.

•Решение нелинейных уравнений.

•Линейное программирование.

•Квадратичное программирование.

•Условная минимизация нелинейных функций.

•Методы минимакса.

•Многокритериальная оптимизация.

Рассматриваемый пакет дает возможности решать задачи минимизации функций, нахождения решений уравнений, задачи аппроксимации («подгонки» кривых под экспериментальные данные).

Различные типы таких задач вместе с применяемыми для их решения функциями пакетаOptimization Toolbox (дальнейшее изложение будет относиться к версии2.0, используемой в составе MATLАВ 5.3.1) приведены в табл. 1.

Таблица 1 Типы задач, решаемых средствами пакета Optimization Toolbox

x, y

F (x) - wg £ goal, c(x) £ 0, ceq(x) = 0 ,

Ax £ b , Aeq x = beq, xL £ x £ xU

векторные аргументы;

·f(a), f(x) – скалярные функции; F(x), c(x), ceq(x), K(x,w) – векторные функции;

·A, Aeq, C, H – матрицы;

·B, beq, d, f, w, goal, xdata, ydata – векторы;

·xL, xU – соответственно, нижняя и верхняя границы области изменения аргумента.

1.2.Применяемые алгоритмы

Врамках пакетаOptimization Toolbox все задачи оптимизации делятся на две группы: задачи малой и средней размерности и задачи большой размерности. Соответственно, такое же деление принято для алгоритмов решения данных задач. Разумеется, это не означает, что для решения задач средней размерности нельзя применять алгоритмы большой размерности и наоборот. Просто алгоритмы той или иной группы более эффективны для задач своей размерности.

Впакете Optimization Toolbox реализован широкий набор алгоритмов для решения задач оптимизации средней и малой размерности. Основными для задач без ограничений

достижения цели и полубесконечной оптимизации использованы алгоритмы квадратичного программирования.

Задачи, сводящиеся к нелинейным МНК, решаются с

параметрических границ xL , xU . Общая формулировка задачи

параметрической оптимизации представляется следующим образом: требуется найти вектор х, обеспечивающий

min f (x)

xÎR''

при ограничениях

gi (x) = 0, i = 1,2,..., me ,

gi (x) £ 0, i = me +1,...,m, xL £ x £ xU ,

где х – вектор оптимизируемых параметров (x Î Rn ), f (x) – скалярная целевая функция(критерий) векторного аргумента

151

( f (x) : R n ® R) , gi (x) – также некоторые скалярные функции

векторного аргумента (заметим, что задача максимизации сводится к задаче минимизации заменой f(х) на -f(х)).

Эффективность и точность решения данной задачи зависит как от числа параметров и ограничений, так и от вида целевой функции. При линейных ограничениях и целевой функции приведенная задача оптимизации называется задачей линейного программирования, при линейных ограничениях, но при квадратичной(по аргументам) целевой функции – задачей квадратичного программирования, в общем случае это задача нелинейного программирования.

1.4. Безусловная оптимизация

Существующие алгоритмы безусловной оптимизации могут быть разделены на две группы— алгоритмы, базирующиеся на использовании производных минимизируемой функции (градиентные и методы второго порядка), и алгоритмы, использующие только значения функции (безградиентные).

Безградиентные методы (например, симплексный метод Нелдера — Мида) более пригодны для задач, где минимизируемая функция является существенно нелинейной или имеет разрывы. Градиентные методы (методы первого порядка) обычно эффективны в случаях целевых функций, непрерывных вместе с первыми производными. Методы второго порядка, такие как метод Ньютона, применяются реже, поскольку требуют больших вычислительных затрат для расчета матриц вторых производных.

Градиентные методы используют информацию о наклоне функции для выбора направления поиска экстремума.

В одном из таких методов— наискорейшего спуска — на каждой итерации движение к точке минимума осуществляется в направлении - Ñf (x) (где Ñf (x) – вектор-градиент целевой функции f(х)). Этот метод весьма неэффективен в ситуациях, когда поверхность целевой функции имеет узкие«овраги»,

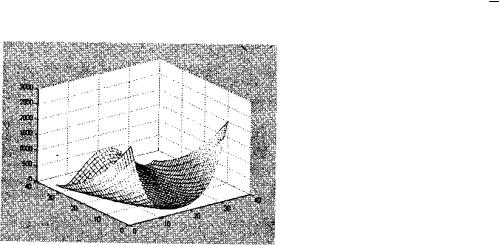
как, например, у известной функции Розенброка

f (x) = 100(x1 - x22 )2 + (1 - x1 ) 2 .

Поверхность этой функции приведена на рис. 1.

Рис. 1. Графическое представление функции Розенброка

Минимальное значение данной функции, как нетрудно

экстремума даже после сотен и тысяч итераций.

Отметим, что указанную функцию из-за своеобразной формы ее линий равного уровня часто называют«банановой» функцией (как видно, банановыми бывают не только республики!) и используют как тестовую при проверке эффективности различных оптимизационных алгоритмов.

функцией, при этом на каждой итерации решается задача локальной минимизации

153

min 1 xT Hx + cT x + b ,

x 2

где Н — симметричная и положительно определенная матрица вторых частных и смешанных производных(матрица Гессе, или гессиан), с — постоянный вектор, b — константа.

Оптимальное решение приведенной зада соответствует нулевым значениям первых производных, то есть

Ñf (x* ) = Hx* + c = 0 ,

откуда

x* = -H -1c .

где

sk = xk +1 - xk ,

qk = Ñf (xk +1 ) - ÑF (xk ) .

Заметим, что более удобно иметь аппроксимацию не

последнем векторы q заменены на векторы s и наоборот.

1.6. Алгоритмы Ньютона-Гаусса и Левенберга-Марквардта

матрица первых частных производных вектор-функции F(х) по векторному аргументу х, а не определитель этой матрицы, как обычно принято в математической литерат; будрем придерживаться терминологии документации пакета), lk —

параметр алгоритма, определяемый в процессе линейной (скалярной) оптимизации вдоль выбранного направления.

1.7.Минимизация при наличии ограничений

Взадачах оптимизации с ограничениями(см. табл. 1) обычный подход к нахождению решения состоит в замене исходной задачи с ограничениями на задачу без ограничений (задачу безусловной оптимизации), например, с помощью метода штрафных функций. В настоящее время, однако, более

m

L(x, l) = f (x) + åli Ñgi (x) ,

i=1

так что на каждой итерации решается задача оптимизации

156

Решение данной вспомогательной задачи производится - мо дификацией метода сопряженных градиентов, так называемого

подробности о которых можно выяснить в справочной системе

MATLAB.

159

Таблица 2 Имена и значения опций функций пакета Optimization Toolbox

Опции, используемые для алгоритмов как средней, так и большой размерности