
Учебное пособие 927
.pdfФГБОУВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Сети и системы передачи информации»
для студентов специальностей 090301 «Компьютерная безопасность», 090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем»
очной формы обучения
Воронеж 2014
Составитель канд. техн. наук И. В. Гончаров
УДК004.056.5
Методические указания к практическим занятиям по дисциплине «Сети и системы передачи информации» для студентов специальностей 090301 «Компьютерная безопасность», 090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем» очной формы обучения / ФГБОУВПО «Воронежский государственный технический университет»; сост. И. В. Гончаров. Воронеж, 2014. 27 с.
Методические указания посвящены исследованию и пониманию наиболее современных способов передачи (кодирования и модуляции) и приема (декодирования и демодуляции) информации, вопросов организации и функционирования систем электросвязи.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2013 и содержатся в файле Гончаров_ПЗ_СИСПИ.pdf.
Ил. 3. Библиогр.: 9 назв.
Рецензент д-р техн. наук, проф. А.Г. Остапенко
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУВПО «Воронежский государственный технический университет», 2014
Практическое задание №1 Дискретизация непрерывного сигнала
Ключевые слова: дискретный сигнал, теорема Котельникова, наивысшая частота, спектральная сигнала, спектр функции, ряд Фурье, квадратично интегрируемая функция, число степеней свободы сигнала.
Цель: научиться переходить от аналоговой формы сигнала к дискретной форме, используя теорему Котельникова и основные формулы дискретных сообщений.
Задачи:
научиться использовать теорему Котельникова;
научиться анализировать полученный дискретный сигнал;
научиться применять ряд Фурье для анализа дискретного сигнала.
Теоретические сведения
Информация передается, и храниться в виде сообщений. Под сообщением понимают совокупность знаков или первичных сигналов содержащих информацию. Иначе говоря, сообщение - это информация представленная в какой-либо форме. Для того чтобы сообщение можно было передать получателю, необходимо воспользоваться некоторым физическим процессом, способным с той или иной скоростью распространяться от источника к получателю сообщения. Изменяющийся во времени физический процесс, отражающий передаваемое сообщение называется сигналом [1].
В зависимости от того, какие значения могут принимать аргумент (время t) и уровни сигналов их делят на 4 типа:
1) Непрерывный или аналоговый сигналы. Они определены для всех моментов времени и могут принимать все значения из заданного диапазона.
2)Дискретизированный или дискретно непрерывные сигналы. Они определены лишь в отдельные моменты времени
имогут принимать любые значения уровня
3)Дискретные по уровню или квантованные сигналы. Они определены для всех моментов времени и принимают лишь разрешенные значения уровней отделенные отдруг друга на величину шага квантования Δx=xk+1+xk.
4)Дискретные по уровню и по времени сигналы. Они определены лишь в отдельные разрешенные моменты времени
имогут принимать лишь разрешенные значения уровней [2]. Замена непрерывного сигнала совокупностью выборок
(без потери информации) основана на теореме отсчетов (теорема Котельникова): если наивысшая частота в спектре оригинала s(t) меньше чем частота дискретизации Fm, то сигнал s(t) полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга не более чем на
1/2Fm сек.
В соответствии с этой теоремой сигнал s(t), ограничен-
ный по спектру наивысшей частотой |
|
ь 2 Fm , может быть |
||||||||||
представлен рядом: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
sin |
|
(t |
|
n |
) |
|
|||
|
n |
m |
2Fm |
|
||||||||
|
|
|
|
|
||||||||
s(t) s( |
) |
|
|
|
|
|
s(n t) n (t) . (1.1) |
|||||
2Fm |
m (t |
|
n |
|
) |
|
||||||
n |
|
|
n |
|||||||||
2Fm
В этом выражении l/2Fm =∆tобозначает интервал между двумя отсчетными, as(n/2Fm) = s(n∆t) — выборки функции s(t) в моменты времени t= n∆t.
Представление заданной функции s(t) рядом (1.3) иллюстрируется рис. 1.
2
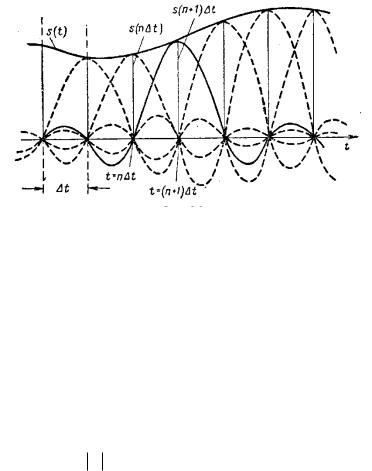
Рис. 1. Представление сигнала в виде ряда Котельникова Функция вида
n |
(t) |
sin m |
(t n t) |
(1.2) |
||
m |
(t n t) |
|||||
|
|
|
||||
обладает следующими свойствами:
в точке t= n∆t φn(n∆t) = 1, а в точках t=k, где k — любое целое, положительное или отрицательное число, отличное от п, φn(k∆t) = 0;
спектральная плотность функции φ0(t) равномерна в полосе частот m и равна 1/2Fm=π/Ωm. Так как функ-
ция φn(t) отличается от φ0(t) только сдвигом на оси времени на величину n∆t, то спектральная плотность функции φn(t).
|
1 |
e in t te in t , при |
|
|
|
|
|
|
|
|
|||
|
|
|
m |
m |
|
|
|
|
|||||
|
2Fm |
|
|
|
|
|
|
|
|
|
|||
Фn |
|
|
|
|
|
|
|
|
|
. (1.3) |
|||
() |
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
, при |
|
|
и |
|
|
. |
|
|
|||
|
|
|
|
|
|
m |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|

Модуль этой функции изображен на нижней части рис. 2 (сплошной линией).
Рис. 2. Связь между спектром сигнала s(t) и спектром функции n (t)
Ряд (1.1) точно определяет заданный сигнал s(t) в точках отсчета, поскольку коэффициентами ряда являются сами выборки из функции, т. е. величины s(n∆t). Коэффициентами ряда (1.1) являются выборки функции s(t) в точках t = n∆t.
Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции s(t), ряд (1.1) сходится к функции s(t) при любом значении t.
Если взять интервал между выборками ∆t' меньшим, чем ∆t=1/2Fm, то ширина 2F'm спектра Ф'n(Ω) функции φ'n(t) будет больше, чем у спектра S(Ω) сигнала s(t) (рис. 1), но это не отразится на величине коэффициентов сп. Модуль функции Ф'n(Ω) изображен на рис.1.1 пунктиром.
При увеличении же ∆t'' по сравнению с ∆t спектр Ф''n(Ω) функции φ''n(t) (на рис. 2 показан штрих-пунктиром) становится уже, чем спектр сигнала s(t),.
4

Итак, сокращение интервалов между выборками по сравнению с величиной 1/2Fm допустимо, но бесполезно. Увеличение же интервала сверх величины 1/2Fm недопустимо.
Рассмотрим теперь случай, когда длительность сигнала s(t) конечна и равнаТ, а полоса частот по-прежнему равна Fm. Эти условия, строго говоря, несовместимы, так как функция конечной длительности обладает теоретически бесконечно широким спектром [2]. Практически, однако, всегда можно определить наивысшую частоту спектра Fmтак, чтобы «хвосты» функции времени, обусловленные отсеканием частот, превышающих Fm, содержали пренебрежимо малую долю энергии по сравнению с энергией заданного сигнала s(t). При таком допущении, если имеется сигнал длительностьюТс полосой частот Fm, общее число независимых параметров т. е. значений s(n∆t), которое необходимо для полного задания сигнала, очевидно, равно
N |
T |
1 2F T 1, |
(1.4) |
t m
при T 1 можно считать N = 2FmT. При этом выражение (1.3)t
принимает следующий вид
|
n FmT |
sin m |
(t n t) |
|
|
|
s(t) |
s(n t) |
. |
(1.5) |
|||
m (t n t) |
||||||
|
n FmT |
|
|
|||
Число N иногда называют числом степеней свободы сигнала s(t) так как даже при произвольном выборе значений s(n∆t) сумма вида (1.5) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала. Число N иногда называют также базой сигнала.
В ряде случаев встречается необходимость представления сигнала с помощью частотных выборок спектральной функции S(Ω), а не временных выборок функции s(t). Для функции S(Ω) можно составить ряд, аналогичный выражению
5

(1.1). Это нетрудно сделать на основании взаимной заменимости переменных tи Ω в преобразованиях Фурье. Применительно к выражению (1.1) это означает, что tдолжно быть заменено на Ω, 2Ωm наТ, 2Fmна Т/2π; ∆t= 1/2Fтна ∆Ω = 2π /Т. Таким образом получается
|
F T |
|
|
|
|
|
|
sin |
T |
( n ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
m |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
S ( ) |
|
S (n ) |
|
|
|
|
|
|||||||||||
|
T |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(1.6) |
|||||||
|
n FmT |
|
|
|
|
|
|
|
2 ( n ) |
|||||||||
|
|
|
|
T |
|
|
|
|
|
2 |
|
|
|
|||||
F T |
|
|
|
sin |
( n |
) |
|
|
||||||||||
|
2 |
|
2 |
|
|
|
|
|||||||||||
m |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||||
= S (n |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
T |
|
T |
|
|
|
|
|
2 |
|
|
||||||||
n FmT |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 ( n T ) |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
Если ранее временной интервал между двумя соседними выборками должен был не превышать 2π/2Ωm,то теперь частотный интервал не должен превышать 2π/Т. При ширине спектра 2 Ωm, охватывающей область частот -Ωm<Ω<Ωm, число
выборок равно 2 ь 1 2FmT 1, как и при представлении
сигнала рядом (1.1).
2
В общем случае выборки S n являются комплекс-
T
ными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра — действительная и мни-
2
мая части S n (или модуль и аргумент). Таким образом,
T
общее число параметров получается вдвое большим, чем при
|
|
1 |
|
временном представлении сигнала, когда выборки |
S n |
|
|
|
|||
|
|
|
|
|
|
2Fm |
|
— действительные числа. Избыточность представления сигнала в частотной области легко устраняется, если учесть, что
6
|
2 |
|
n |
2 |
||
S n |
|
и |
S |
|
являются комплексно-сопряженными |
|
|
T |
|
|
T |
||
числами, так что задание одной из них однозначно определяет другую. Таким образом, число независимых параметров или
степеней свободы сигнала равно 2FmT 1, как и при пред-
ставлении сигнала во временной области.
Энергию и среднюю мощность сигнала нетрудно выразить через заданную последовательность временных выборок.
|
|
FmT |
|
|
|
|
|
|
|
|
|
|
|
FmT |
|
||
E |
cn2 |
|
|
|
|
|
|
|
2 |
|
s(n t) 2 , |
(1.7) |
|||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
n FmT |
|
|
|
|
|
|
|
|
|
|
m n FmT |
|
|||
|
|
|
E |
|
1 |
|
|
|
|
FmT |
|
|
|||||
s2 (t) |
|
|
|
|
|
s(n t) 2 . |
(1.8) |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
T |
2F T |
n FmT |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
||||||
Из последнего выражения видно, что средняя за времяТмощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем отсчетным точкам, число которых равно 2FmТ
Задания и контрольные вопросы
Используя формулу непрерывного сигнала данную преподавателем на практическом занятии привести ее к дискретному виду и провести анализ характеристик полученного сигнала. По приведению сигнала к дискретной форме вычислить его энергию и среднюю мощность, через заданную последовательность временных выборок.
При защите результатов практического задания необходимо представить содержащий их отчет и продемонстрировать свои теоретические знания и практические навыки согласно выполненному заданию.
7
Контрольные вопро сы
1.Виды информационных сигналов.
2.Основная идея теоремы Котельникова.
3.Формула теоремы Котельникова.
4.Применение теоремы Котельникова к информационному сигналу.
5.Связь между спектром сигнала и спектром функ-
ции.
6.Представление сигнала с помощью частотных
выборок
7.Вероятные последствия при сужении или увеличении допустимого интервала между выборками.
8.Вычисление энергии дискретного сигнала
9.Вычисление мощности дискретного сигнала.
8
