ФГБОУВПО «Воронежский государственный

технический университет»

Кафедра систем информационной безопасности

Криптографические методы обеспечения информационной безопасности методические указания

к практическим занятиям

по дисциплине “Криптографические методы

и средства ИБ” для студентов специальностей

090102 “Компьютерная безопасность”, 090105 “Комплексное обеспечение информационной безопасности

автоматизированных систем”, 090106 “Информационная

безопасность телекоммуникационных

систем” очной формы обучения

Воронеж 2011

Составители: преп. Н.М. Радько, преп. А.Н. Мокроусов

УДК 681.326

Криптографические методы обеспечения информационной безопасности: методические указания к практическим занятиям по дисциплине "Криптографические методы и средства ИБ" для студентов специальностей 090102 “Компьютерная безопасность”, 090105 “Комплексное обеспечение информационной безопасности автоматизированных систем”, 090106 “Информационная безопасность телекоммуникационных систем” очной формы обучения / ФГБОУВПО «Воронежский государственный технический университет»; сост. Н.М. Радько, А Н. Мокроусов. Воронеж, 2011. 36 с.

Методические указания предназначены для студентов четвертого и пятого курсов, выполняющих практические занятия по изучению основ криптографии. Рассмотрены элементы теории чисел в разделах модулярная арифметика и алгебраические структуры

Методические указания подготовлены в электронном виде в текстовом редакторе MS WORD и содержатся в файле Криптометоды ИБ.doc.

Табл. 8. Ил. 3. Библиогр.: 13 назв.

Рецензент д-р техн. наук, проф. Н.Н. Толстых

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.Г. Остапенко

Издаётся по решению редакционно-издательского совета Воронежского государственного технического университета

 ФГБОУВПО “Воронежский государственный технический университет”, 2011

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1

АЛГОРИТМ ЕВКЛИДА ДЛЯ НАХОЖДЕНИЯ

ОБЩЕГО ДЕЛИТЕЛЯ

Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел [1].

Вспомним математику. Наибольший общий делитель двух натуральных чисел - это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:

НОД(12, 18) = 6.

Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом: Дано: М, N Найти: НОД(М, N).

В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.

Идея алгоритма Евклида

Идея этого алгоритма основана на том свойстве, что если M>N, то

НОД(М, N) = НОД(М - N, N).

Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.

Легко доказать это свойство. Пусть К - общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n - натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К - делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N, в том числе и наибольший общий делитель.

Второе очевидное свойство:

НОД(М, М) = М.

Для "ручного" счета алгоритм Евклида выглядит так:

1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;

2) заменить большее число разностью большего и меньшего из чисел;

3) вернуться к выполнению п. 1.

Рассмотрим этот алгоритм на примере М=32, N=24:

Получили: НОД(32, 24) =НОД(8, 8) = 8, что верно.

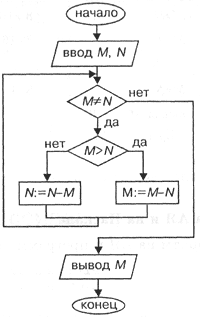
На рис.1 приведена блок-схема алгоритма Евклида.

Рис.1. Блок-схема алгоритма Евклида

С

2

труктура алгоритма - цикл с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.

Ниже представлена табл.1 алгоритма для исходных значений М = 32, N = 24.

Таблица 1

Шаг	Операция	M	N	Условие
1	ввод М	32
2	ввод N		24
3	M ¹ N			32 ¹ 24, да
4	M>N			32>24, да
5	M:=M-N	8
6	M ¹ N			8 ¹ 24, да
7	M>N			8>24, нет
8	N:=N-M		16
9	M ¹ N			8 ¹ 16, да
10	M>N			8>16, нет
11	N:=N-M		8
12	M ¹ N			8 ¹ 8, нет
13	вывод M	8
14	конец

В итоге получился верный результат.

Контрольные вопросы:

1. Что такое наибольший общий делитель двух натуральных чисел?

2. На каком свойстве основана идея алгоритма Евклида?

3. Какова блок-схема алгоритма Евклида?

3

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2

РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА

При заданных неотрицательных целых [2,3,9,10] числах а и b этот алгоритм определяет вектор

(u₁, u₂, u₃),

такой, что

а * u₁+ b * u₂ = u₃ = НОД (a, b).

В процессе вычисления используются вспомогательные векторы (v₁, v₂, v₃), (t₁, t₂, t₃). Действия с векторами производятся таким образом, что в течение всего процесса вычисления выполняются соотношения

а * t₁ + b * t₂ = t₃,

a * u₁ + b * u₂= u₃,

a * v₁ + b * v₂ = v₃.

Для вычисления обратной величины a^-1 (mod n) используется частный режим работы расширенного алгоритма Евклида, при котором Ь = n , НОД (а, n)=1, и этот алгоритм определяет вектор

(u₁, u₂, u₃),

такой, что

u₃ = 1, a * u₁ + n * u₂ = НОД (а, n) = 1,

(а * u₁+ n * u₂) mod n а * u₁(mod n) 1.

a^-1 (mod n) u₁ (mod n).

Шаги алгоритма :

1. Начальная установка . Установить (u₁, u₂, u₃) := (0, 1, n),

(v₁, v₂, v₃) := (1, 0, a).

2. u₃ = 1?. Если u₃ = 1, то алгоритм заканчивается.

3. Разделить, вычесть. Установить q :=[ u₃ / v₃ ]. Затем установить

(t₁, t₂, t₃) := (u₁, u₂, u₃) - (v₁, v₂, v₃) * q,

(u₁, u₂, u₃) := (v₁, v₂, v₃),

(v₁, v₂, v₃) := (t₁, t₂, t₃).

Возвратиться к шагу 2.

П

4

ример 1 . Заданы модуль n = 23 и число а = 5. Найти обратное число a^-1 (mod 23), т. е. x=5^-1 ( mod 23).

Используя расширенный алгоритм Евклида, выполним вычисления, записывая результаты отдельных шагов в табл.2.

Таблица 2

q	u1	u2	u3	v1	v2	v3
-	0	1	n = 23	1	0	а = 5
4	1	0	5	-4	1	3
1	-4	1	3	5	-1	2
1	5	-1	2	-9	2	1
-	-9	2	1

При u₃= 1, u₁= -9, u₂= 2

(а * u₁ + n * u₂ ) mod n = (5 * (-9) + 23 * 2) mod 23 =

= 5*(-9) mod 23 1,

a^-1 (mod n) = 5^-1 (mod 23) = (-9) mod 23 = (-9 + 23) mod 23 = 14.

Итак , х = 5^-1(mod 23) 14 (mod 23) = 14.

Для решения более сложных сравнений

а * х b (mod n), т. е. Ь≠1, х = ?

используется следующий прием. Сначала решают сравнение

а * у 1(mod n), т. е. определяют

у = a^-1( mod n), а затем находят

х = a^-1 b (mod n) = у * b (mod n).

Пример 2. Найти х для сравнения

5 * х 9 (mod 23).

Сначала решаем сравнение

5 * y 1(mod 23).

Получаем у = 5^-1(mod 23) = 14. Затем находим

х = 5^-1 * 9 (mod 23) = 14 * 9 (mod 23) = 126 (mod 23) 11 (mod 23),

x = 11.

Контрольные вопросы:

4. Какой вектор определяет расширенный алгоритм Евклида?

5. Каковы шаги расширенного алгоритм Евклида?

5

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3

ВЫЧИСЛЕНИЕ ОБРАТНЫХ ВЕЛИЧИН

В арифметике действительных чисел [7, 8] нетрудно вычислить мультипликативную обратную величину а^-1 для ненулевого а:

а^-1 =1/а или а * а^-1 = 1.

Например, мультипликативная обратная величина от числа 4 равна 1/4, поскольку

4 * 1/4 = 1.

В модулярной арифметике вычисление обратной величины является более сложной задачей. Например, решение сравнения

4 * x 1( mod 7)

эквивалентно нахождению таких значений х и к, что

4 * х 7 * к +1,

где х и к - целые числа.

Общая формулировка этой задачи - нахождение такого целого числа х , что

a * x (mod n)=1.

Можно также записать

а^-1 x (mod n).

Решение этой задачи иногда существует, а иногда его нет . Например, обратная величина для числа 5 по модулю 14 равна 3, поскольку

5*3=15 1 (mod 14).

С другой стороны, число 2 не имеет обратной величины по модулю 14.

Вообще сравнение a^-1 x (mod n) имеет единственное решение, если а и n - взаимно простые числа.

Если числа а и n не являются взаимно простыми, тогда сравнение a^-1 x ( mod n ) не имеет решения.

Сформулируем основные способы нахождения обратных величин. Пусть целое число aє{0, 1, 2, ..., n -1}. Если НОД (а, n) = 1, то a * i (mod n) при i = 0, 1, 2, ..., n-1 является перестановкой множества {0, 1, 2, ..., n -1}.

Например, если а = 3 и n = 7(НОД (3,7)=1), то

3 * i ( mod 7) при i = 0, 1, 2, ..., 6

я

6

вляется последовательностью 0, 3, 6, 2, 5, 1, 4, т. е. перестановкой множества {0, 1, 2 .... 6}.

Это становится неверным, когда НОД (а , n)≠1. Например, если а = 2 и n =6, то

2 * i ( mod 6) 0, 2, 4, 0, 2, 4 при i = 0, 1, 2, ..., 5.

Если НОД (а, n)=1, тогда существует обратное число а^-1, 0<а^-1<n , такое, что

а * а^-1 1(mod n).

Действительно, a * i (mod n) является перестановкой 0,1, ..., n-1, поэтому существует i, такое, что

а * i 1(mod n).

Как уже отмечалось, набор целых чисел от 0 до n-1 называют полным набором вычетов по модулю n. Это означает, что для любого целого числа а(а>0) его вычет r=a (mod n) - это некоторое целое число в интервале от 0 до n-1.

Выделим из полного набора вычетов подмножество вычетов, взаимно простых с n . Такое подмножество называют приведенным набором вычетов.

Пример. Пусть модуль n = 11 - простое число. Полный набор вычетов по модулю 11

{0, 1, 2, ..., 10}.

При формировании приведенного набора вычетов из них удаляется только один элемент - 0. Приведенный набор вычетов по модулю 11 имеет 11-1=10 элементов.

Вообще приведенный набор вычетов по модулю простого числа n имеет n-1 элементов.

Пример. Пусть модуль n =10. Полный набор вычетов по модулю n =10

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Из них только 1, 3, 7, 9 не имеют общего сомножителя с числом 10. Поэтому приведенный набор вычетов по модулю 10 равен {1, 3, 7, 9}. При формировании этого приведенного набора были исключены элементы:

0	(1 элемент)
кратные 2	(4 элемента)
кратные 5	(1 элемент),

т

7

. е. всего шесть элементов. Вычитая их из 10, получаем 10-1-4-1=4, т. е. четыре элемента в приведенном наборе.

Для произведения простых чисел p*q=n приведенный набор вычетов имеет (р - 1)(q - 1) элементов. При n = p*q = 2*5= 10 число элементов в приведенном наборе

(р-1)(q-1) = (2-1)(5-1) = 4.

Пример. Приведенный набор вычетов по модулю 27= З³ имеет 18

элементов:

{1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26}.

Из полного набора вычетов исключены элементы, кратные 3 (всего девять элементов). Для модуля в виде простой степени n^r приведенный набор вычетов имеет n^r-1 1(n-1) элементов.

При n = 3, r = 3 получаем З^3-1(3-1)=3² *2=18.

Функция Эйлера (n) характеризует число элементов в приведенном наборе вычетов (табл.3).

Таблица 3

Модуль n	Функция (n)
n - простое n2 ... nr	n - 1 n (n - 1) ... nr-1 (n - 1)
р * q ( p, q - простые ) ...	(p-1)(q-1) ...

Иначе говоря, функция (n) - это количество положительных целых, меньших n, которые взаимно просты с n.

Малая теорема Ферма: если n - простое и НОД (а, n) = 1, то

a^n-1 1(mod n).

Согласно обобщению Эйлером малой теоремы Ферма имеем: если НОД (а, n)= 1, то

a ⁽ⁿ⁾ 1(mod n).

Если n - простое число, то предыдущий результат, учитывая , что (n) = n-1, приводится к виду (малой теоремы Ферма)

a^n-1 1(mod n).

О

8

сновные способы нахождения обратных величин

a^-1 1( mod n).

•  Проверить поочередно значения 1, 2 ,..., n -1, пока не будет найден a^-1 1(mod n), такой, что a*a^-1 (mod n) 1 .

•  Если известна функция Эйлера (n), то можно вычислить

a^-1(mod n) a ^(n)-1 (mod n),

используя алгоритм быстрого возведения в степень.

3. Если функция Эйлера (n) не известна, можно использовать расширенный алгоритм Евклида.

Проиллюстрируем эти способы на числовых примерах .

1. Поочередная проверка значений 1, 2, ..., n-1, пока не будет найден x=a^-1 (mod n), такой что a * x 1(mod n).

Пусть n = 7, а = 5. Требуется найти x = a^-1 (mod n).

a*x 1(mod n) или 5*x 1 (mod 7).

n-1 = 7-1 = 6.

Получаем x = 5^-1 (mod 7) = 3.

Результаты проверки сведены в табл.4.

Таблица 4

x	5 * х	5 * х (mod 7)
1	5	5
2	10	3
3	15	1
4	20	6
5	25	4
6	30	2

2. Нахождение a^-1 (mod n), если известна функция Эйлера (n). Пусть n=7, а=5. Найти x = a^-1 (mod n) = 5^-1 (mod 7). Модуль n=7 - простое число. Поэтому функция Эйлера (n) = (7) = n-1=6. Обратная величина от 5 по mod 7

a^-1 (mod n) = a ^(n)-1(mod n) = 5^6-1 mod 7 = 5⁵ mod 7 = (5² mod 7)(5³ mod 7) mod 7 = (25 mod 7)(125 mod 7) mod 7 = (4 * 6) mod 7 = 24 mod 7= 3.

И

9

так, x =5^-1 (mod 7) = 3.

3. Нахождение обратной величины a^-1 (mod n) с помощью расширенного алгоритма Евклида.

Алгоритм Евклида можно обобщить способом, который имеет большое практическое значение. При этом способе во время вычисления НОД (а, Ь) можно попутно вычислить такие целые числа u₁, и u₂, что

а * u₁ + b * u₂ = НОД (a, b).

Это обобщение (расширение) алгоритма Евклида удобно описать, используя векторные обозначения.

Контрольные вопросы:

6. Что такое мультипликативная обратная величина?

7. Что такое полный набор вычетов по модулю?

8. В чём смысл малой теоремы Ферма?

10

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4

КВАДРАТИЧНЫЕ ВЫЧЕТЫ

Рассмотрим некоторое простое р>2 и число а<р [2]. Если число а сравнимо с квадратом некоторого числа х по модулю р, т. е. выполняется сравнение x² a (mod p), тогда а называют квадратичным вычетом по модулю р. В противном случае а называют квадратичным невычетом по модулю р.

Если а - квадратичный вычет, сравнение x² a (mod p) имеет два решения: + х и - х, т. е. а имеет два квадратных корня по модулю р.

Все квадратичные вычеты находят возведением в квадрат элементов 1, 2, 3, ..., (р-1)/2.

Не все значения а<р являются квадратичными вычетами. Например, при р=7 квадратичные вычеты это 1, 2, 4:

1² =1 1(mod 7),

2² = 4 4(mod 7),

3² = 9 2(mod 7),

4² = 16 2(mod 7),

6² = 36 1(mod 7).

Заметим, что каждый квадратичный вычет появляется в этом списке дважды. Не существует никаких значений х, которые удовлетворяли бы любому из следующих уравнений:

x² 3(mod 7),

x² 5(mod 7),

x² 6(mod 7),

Числа 3, 5 и 6 - квадратичные невычеты по модулю 7. Можно доказать, что существует точно (р -1)/2 квадратичных вычетов по модулю р и (р-1)/2 квадратичных невычетов по модулю р.

Если а - квадратичный вычет по модулю р, то а имеет точно два квадратных корня: один корень между 0 и (р-1)/2, другой корень между (р-1)/2 и (р-1).

Один из этих квадратных корней также является квадратичным вычетом по модулю р; он называется главным квадратным корнем.

Пример. Вычисление квадратных корней при р=7 представлено в табл.5.

11

Таблица 5
	Корни
х2 a(mod 7)	x1	x2
12 1(mod 7) 22 4(mod 7) 32 2(mod 7)	+1 +2 +3	-1 = -1 + 7 = 6 -2 = -2 + 7 = 5 -3 = -3 + 7 = 4

Если n - произведение двух простых р и q, т. е. n = p * q, то существуют точно

(p-1)(q-1)/4

квадратичных вычетов по модулю n, взаимно простых с n. Например, по модулю 35 (р=5, q=7, n=5*7=35) существуют

(5-7)(7-1)/4 = 4*6/4 = 6

квадратичных вычетов: 1, 4, 9, 11, 16, 29, взаимно простых с 35.

Контрольные вопросы:

9. Что такое квадратичный невычет по модулю?

10. Как находят квадратичные вычеты?

11. Что такое главный квадратный корень?

12

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5

КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ

Любое неотрицательное целое число, не превосходящее произведения модулей, можно однозначно восстановить, если известны его вычеты по этим модулям [2]. Этот результат был известен еще в древнем Китае и носит название китайской теоремы об остатках. Теорема была предложена китайским математиком первого века Сун Це. Китайская теорема об остатках является мощным криптографическим инструментом.

Китайская теорема об остатках формулируется следующим образом.

Пусть m₁, m₂, ..., m_t - модули (целые числа, большие 1), которые являются попарно взаимно простыми, т. е. HOД (m_i, m_j)=1 при i ≠ j .

Пусть a₁, a₂, ..., a_t - тоже целые числа, 0 ≤ a_i ≤ m_i.

Пусть M = m₁ * m₂ *...* m_t- произведение всех m_i. Обозначим М_i = М /m_i

И пусть N_i будет обратным к M_i (mod m_i), i=1, 2, ..., t, т. е. M_i * N_i 1(mod m_i).

Так как HOД (M_i, m_i) = 1, то обратный элемент N_i существует и легко находится из алгоритма Евклида из соотношения

M_i * N_i + m_i * n _i = 1, i = 1, 2, ..., t.

Сравнения x a_i (mod m_i), i = 1, 2, ..., t, имеют в интервале [0, М-1] единственное общее решение

x= a_i * N_i * M_i (mod M).

Рассмотрим частный случай. Пусть M = m₁ * m_2, где m₁, m₂ - взаимно простые числа. Тогда для произвольных целых a₁< m₁ и a₂<m₂ существует единственное число х, х<М, такое, что

х a₁(mod m₁) и x = a₂ (mod m₂).

Чтобы найти значение решения х, сначала используют алгоритм Евклида для вычисления значений N_i и N₂, таких, что

N₁ * M₁ 1 (mod m₁) и N₂ * М₂ 1 (mod m₂).

Здесь M₁ = M / m₁ = m₁* m₂ / m₁= m₂

M₂ = M / m ₂ = m₁

Затем вычисляют значение

x

13

= (a₁* N₁* M₁ + a₂* N₂* M₂)(mod M).

Пример. Решить систему из двух сравнений

x 1(mod 5),

х 10 (mod 11)

и найти общее решение х по модулю 55. Здесь m₁= 5; m₁= 11; M=m₁* m₂ = 5*11=55; a₁ = 1; a₂=10; M₁= M/m₁=m₂=11; M₂=M/m₂=m₁=5.

Найдем значения N₁ и N₂, обратные к M₁ и M₂ соответственно по mod m₁ и - mod m₂:

M₁* N₁ 1 (mod m₁), 11*N₁ 1(mod 5) => N₁ = 1,

M₂* N₂ 1(mod m₂), 5 * N₂ 1 (mod 11) => N₂ = 9.

Вычисляем общее значение

x = (a₁M₁N₁ + a₂M₂N₂)(mod N) = (1 * 11 * 1 + 10 * 5 * 9)(mod 55) =

= (11 + 450)(mod 55) = 461 (mod 55) = 21 (mod 55).

Итак, x=21(mod 55).

Контрольные вопросы:

12. Как можно восстановить любое неотрицательное целое число, не превосходящее произведения модулей?

13. Какие формулируется китайская теорема об остатках?

14

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6

МОДУЛЯРНАЯ АРИФМЕТИКА

Модулярная арифметика часто изучается в школе как "арифметика часов" [3,11-13]. Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня:

3+14 5 (mod 12)

или

(3+14) mod 12=5

Это арифметика по модулю 12. Обычная запись в модулярной арифметике

a b(mod n)

читается так: "а сравнимо с b по модулю n". Это соотношение справедливо для целых значений a, b и n≠0, если, и только если

а = b + k * n

для некоторого целого к. Отсюда, в частности, следует

n | (а - b).

Это читается как "n делит (а - b)". Если a b(mod n) то b называют вычетом числа а по модулю n. Операцию нахождения вычета числа а по модулю n

a(mod n)

называют приведением числа а по модулю n или приведением по модулю. В нашем примере

(3 +14) mod 12 = 17 mod 12 = 5

или

17 5(mod 12),

число 5 является вычетом числа 17 по модулю 12. Набор целых чисел от 0 до (n-1) называют полным набором вычетов по модулю n. Это означает, что для любого целого a(а>0) его вычет r по модулю n есть некоторое целое число в интервале от 0 до (n-1), определяемое из соотношения

г

15

=а-к*n,

где к - целое число. Например, для n=12 полный набор вычетов:

{0, 1, 2, …, 11}.

Обычно предпочитают использовать вычеты

rє{0,1,2, ... , n-1},

но иногда полезны вычеты в диапазоне целых:

Заметим, что

-12(mod 7) -5(mod 7) 2(mod 7) 9(mod 7) и т.д.

Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности. Фактически мы можем либо сначала приводить по модулю n, a затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n:

(а + b) mod n = [a(mod n) + b(mod n)] mod n, (а - b) mod n = [a(mod n) - b(mod n)] mod n. (а * b) mod n = [a(mod n) * b(mod n)] mod n, [а * (b + с)] mod n = {[а * b(mod n)] + [а * c(mod n)]} mod n.

16

Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата. Для модуля n длиной к бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2к бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов. Вычисление степени числа а по модулю n можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более). Например, если нужно вычислить

a⁸mod n,

не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

(а*а*а*а*а*а*а*а) mod n.

Вместо этого выполняют три малых умножения и три малых приведения по модулю:

((a² mod n)² mod n)² mod n.

Тем же способом вычисляют

a¹⁶ mod n = (((a² mod n)² mod n)² mod n)² mod n.

Вычисление

a^x mod n,

где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х как сумму степеней 2: x = 25₍₁₀₎-> 11001₍₂₎ , поэтому 25 = 2⁴ + 2³ + 2⁰. Тогда

a²⁵ mod n = (а * a²⁴) mod n = (а * а⁸ * a¹⁶) mod n = а * ((а²)²)² * (((a²)²)²)² mod n = ((((а² * *а)²)²)² * a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a² mod n) * a) mod n)² mod n)² mod n)² mod n) * a) mod n

Этот метод уменьшает трудоемкость вычислений до 1,5хк операций в среднем, где к - длина числа в битах. Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n , целесообразно использовать алгоритмы быстрого возведения в степень.

Контрольные вопросы:

14. Как можно выполнить вычисление степени числа а по модулю n?

15. В чём смысл гомоморфного отображения из кольца целых в кольцо целых?

16. Что такое приведение по модулю?

17

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7

ВЫЧИСЛЕНИЯ В КОНЕЧНЫХ ПОЛЯХ

Поле F есть множество, на котором определены операции сложения и умножения, удовлетворяющие требованиям: ассоциативности, коммутативности, дистрибутивности, существования аддитивного 0 и мультипликативной 1, аддитивных обратных и мультипликативных обратных для всех элементов за исключением 0 [2,7].

Конечное поле F (p) с конечным числом р элементов играет важную роль в криптографии. В общем случае число элементов

P = qⁿ,

где q - некоторое простое число и n≠1. Такие конечные поля называют полями Галуа и обозначают GF (qⁿ) или GF (q) при n=1. (Эварист Галуа - французский математик начала XIX века.) Многие криптосистемы базируются на полях Галуа GF (q), где q - большое простое число.

Пример. Поле Галуа GF (5) имеет элементы 0, 1, 2, 3, 4 и описывается таблицами сложения и умножения (табл.6):

										Таблица 6
+	0	1	2	3	4		X	1	2	3	4
0	0	1	2	3	4		1	1	2	3	4
1	1	2	3	4	0		2	2	4	1	3
2	2	3	4	0	1		3	3	1	4	2
3	3	4	0	1	2		4	4	3	2	1
4	4	0	1	2	3

Если q - простое число, то число a є [1, q - 1] является взаимно простым с q, и поэтому обратный элемент а^-1 имеет единственное значение. Тем самым однозначно определяется операция деления.

О

18

бозначим через GF *(q) множество всех ненулевых элементов поля GF (q). Некоторый элемент g из GF *(q) называют образующим или порождающим элементом GF *(q), если для всех а из GF*(q) найдется такое целое х, что g^x = a mod q. Всего имеется φ(q-1) образующих элементов g. Число х называют дискретным логарифмом элемента а по основанию g и модулю q. Вычисление дискретных логарифмов (когда заданы g, а и q) примерно такая же труднорешаемая задача, как и разложение на множители.

Еще один тип поля Галуа, используемый в криптографии, основывается на арифметике по модулю неприводимых многочленов степени n, чьи коэффициенты - целые числа по модулю q, где q - простое. Эти поля Галуа обозначают как GF (qⁿ). Они имеют элементы, которые описываются многочленами степени не выше (n-1) в форме

а (х) = a_n-1X^n-1 + ... + a₁, Х + а₀.

Каждый элемент а (Х) является вычетом по модулю р(Х), где р(Х)- неприводимый многочлен степени n (т. е. р(Х) нельзя разложить на сомножители - многочлены степени меньше n).

Арифметические действия над коэффициентами a_i выполняются по модулю q, а наивысшая степень X равна (n-1), так как выполняется приведение по модулю многочлена р(Х), имеющего старшую степень n.

Особый интерес представляют поля GF (2ⁿ). Здесь коэффициентами а, являются 0 и 1. Поэтому многочлен а(Х) степени не выше (n-1) можно представить как вектор из n двоичных цифр:

a_n-1a_n-2 ... a₁a₀

Каждый из n-битовых векторов соответствует конкретному элементу поля GF (2ⁿ).

Например, поле Галуа GF (2³) имеет элементы:

Таблица 7

Многочлены		Двоичная форма
0		000
1		001
x		010
x + 1		011
x2		100
x2 + 1		101
x2 + x		110
x2 + x + 1		111

Организация вычислений в полях Галуа предполагает знание некоторых свойств многочленов и их корней в двоичном поле GF (2). Кратко приведем некоторые из них:

С

19

войство 1. Ненулевые элементы поля GF (2ⁿ) являются корнями обобщенного многочлена .

Свойство 2. Каждый многочлен р(Х) степени n, неприводимый над полем GF (2), является делителем двучлена , и каждый делитель двучлена , неприводимый над полем GF (2), имеет степень, равную n и менее.

Свойство 3. Все элементы поля GF (2ⁿ) можно получить как совокупность остатков от деления 100...00 на неприводимый многочлен р (Х), входящий в разложение двучлена ( ). Эти остатки - корни двучлена ( ), т. е. обращают его в нуль. Число остатков равно (2ⁿ-1).

Свойство 4. В поле GF (2ⁿ) существует примитивный элемент α, такой, что каждый ненулевой элемент поля GF (2ⁿ) может быть представлен как некоторая степень α, т. е. мультипликативная группа GF (2ⁿ) является циклической.

Пример. Определение элементов α_i поля GF (2⁴). Согласно свойству 1 ненулевые элементы поля GF (2⁴) являются корнями обобщенного двучлена ( ) = (X¹⁵+1). Двучлен (X¹⁵+1) можно представить в виде произведения неприводимых многочленов - сомножителей:

(X¹⁵+1) = P(Х¹) * Р (Х²) * Р₁(Х⁴) * Р₂(Х⁴) * Р₃(Х⁴),

где

P(Х¹) = (X+1), Р(Х²) = Х² + X + 1,

Р₁(Х⁴) = Х⁴ + X + 1, Р₂(Х⁴) = Х⁴ + Х³ +1,

Р₃(Х⁴) = Х⁴ + Х³ + Х² + X + 1

В соответствии со свойством 3 вычислим элементы α_i поля GF (2⁴) как совокупность остатков отделения 100...00 на неприводимый многочлен Р₁(Х⁴) = Х⁴ + X + 1.

Процедура определения остатков

Делят на Р₁(Х⁴) = Х⁴ + X + 1 <--> 10011 единицу с возрастающим числом нулей, т. е. делят одночлены X^j, где j = 0, 1, 2, 3 ... на многочлен (Х⁴ + X + 1). Степени одночленов Х⁰, Х¹, Х², Х³ меньше степени многочлена Р₁(Х⁴), поэтому первые четыре остатка от деления на Р₁(Х⁴) равны делимым, т. е. одночленам Х⁰, Х¹, Х², Х³. Для одночлена Х⁴ <--> 10000 получаем остаток

Для одночлена Х⁵ <--> 100000 получаем остаток

С

20

хема вычисления остатков:

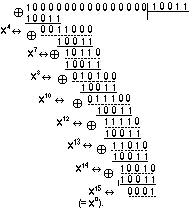
Вычисленные остатки и нулевые элементы α₀ - α₁₄ поля Галуа GF (2⁴) сведены в табл.8.

Таблица 8

Xi	Остаток	αi
Х0	0001	α0
X1	0010	α1
X2	0100	α2
X3	1000	α3
X4	0011	α4
X5	0110	α5
X6	1100	α6
X7	1011	α7
X8	0101	α8
X9	1010	α9
X10	0111	α10
X11	1110	α11
X12	1111	α12
X13	1101	α13
X14	1001	α14

Поле Галуа GF (2⁴) построено как поле многочленов с коэффициентами 0 и 1 по модулю неприводимого многочлена:

Р

21

(Х⁴)=Х⁴ + Х + 1<--> 10011.

В поле Галуа GF (2ⁿ) определены четыре алгебраические операции. Операции сложения и вычитания выполняются как опера­ ции поразрядного сложения по модулю 2; операция умножения элементов поля выполняется как умножение соответствующих многочленов с приведением по модулю неприводимого многочлена Р (Х), т. е. многочлена, по модулю которого построены элементы поля GF (2ⁿ).

Пример. α₅ = 0110, α₆ = 1100, α₅+ α₆ = 1010, так как

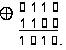
Пример. α₁₄ = 1001,

α₁₄ * α₁₄ = α²₁₄= α₁₃ по mod Р₁(Х⁴) <-->1 0 0 1 1.

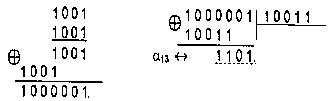
Чтобы выполнить деление элемента b на элемент а в поле модулю Р (Х), сначала находят обратный элемент a^-1(mod P (X)), а затем вычисляют

b * a^-1(mod P (X)).

Каждый двоичный вектор длиной n, исключая 0, является взаимно простым с неприводимым многочленом Р (Х) независимо от значения Р (Х). Поэтому число вычетов, взаимно простых с Р(Х), равно φ(Р(Х)) = 2ⁿ - 1 (расширение функции Эйлера для многочленов). Поэтому

a^-1= a^φ(P(X))-1 mod Р(Х) = mod P(Х)

Пример. Пусть a = 100 и P(X) = 1011 в поле GF (2³).

a^-1= (mod 1011) = 100⁶ (mod 1011) = 100² * 100⁴(mod 1011). 100² (mod 1011) = 10000 10110 = 110

или

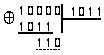
1

22

00⁴ (mod 1011) = 110² (mod 1011) = 010

или

100² * 100⁴ (mod 1011)= 110 * 010 (mod 1011) = 1100 (mod 1011) = 111

или

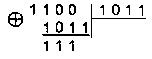
Итак, a^-1 = 111. Проверка: a=100, a^-1 = 111, P(X)=1011, a*a^-1=110*100=11100

т. е. a*a^-1(mod 1011) = 1.

Достоинства вычислений в поле GF (2ⁿ):

•  Все элементы поля Галуа имеют конечный размер, деление элементов не имеет каких-либо ошибок округления.

•  Сложение и вычитание элементов поля GF (2ⁿ) не требует деления на модуль.

•  Алгоритмы вычислений в поле GF (2ⁿ) допускают парал­ лельную реализацию.

•  Для поля GF (2ⁿ) обычно применяют в качестве модуля трех­ член Р (Хⁿ) = Хⁿ + Х + 1.

Длинная строка нулей между коэффициентами при Xⁿ и X обеспечивает более простую реализацию быстрого умножения (с приведением по модулю). Трехчлен Р (Хⁿ ) должен быть неприводимым и примитивным.

Т

23

рехчлен Р (Хⁿ)= Хⁿ + Х + 1 является примитивным для следующих значений n (n<1000):

1, 3, 4, 6, 9, 15, 22, 28, 30, 46, 60, 63, 127, 153, 172, 303, 471, 532, 865, 900.

Контрольные вопросы:

17. Что такое конечное поле?

18. В чём смысл свойств многочленов и их корней в двоичном поле GF (2)?

19. Каковы достоинства вычислений в поле GF (2ⁿ)?

24

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8

ТЕСТИРОВАНИЕ ПРОСТОТЫ ЧИСЛА

МЕТОДОМ ПЕРЕБОРА ДЕЛИТЕЛЕЙ

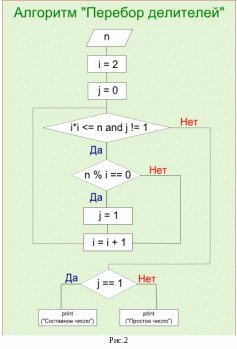
Перебор делителей – это алгоритм, применяемый для определения, какое число перед нами: простое или составное [4].

Алгоритм заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню тестируемого числа. Если хотя бы один делитель делит тестируемое число без остатка, то оно является составным. Если у тестируемого числа нет ни одного делителя, делящего его без остатка, то такое число является простым. Блок-схема данного алгоритма представлена на рис.2.

Контрольные вопросы:

20. В чем смысл алгоритма перебора делителей?

21. Какова блок-схема алгоритма перебора делителей?

25

26

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9

РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ

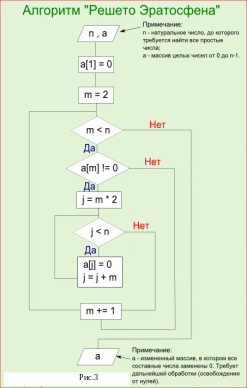
Разложить число на множители - значит найти его простые сомножители [4].

10 = 2*5

60 = 2*2*3*5

252601=41*61*101

2113- 1 =3391*23279*65993*1868569*1066818132868207

Разложение на множители является одной из древнейших проблем теории чисел. Этот процесс несложен, но требует времени. Это пока остается так, но ряд сдвигов в этом искусстве все же произошел.

Решето Эратосфена – это алгоритм нахождения простых чисел до заданного числа n. В процессе выполнения данного алгоритма постепенно отсеиваются составные числа, кратные простым, начиная с 2. Блок-схема данного алгоритма представлена на рис.3.

Контрольные вопросы:

22. Что означает разложить число на множители?

23. В чём смысл решета Эратосфена?

27

28

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №10

СИМВОЛЫ ЛЕЖАНДРА И ЯКОБИ

Символ Лежандра, L(a,/p), определен, если a - это любое целое число, а p - простое число, большее, чем 2. Он равен 0, 1 или -1 [6].

L(a,p) = 0, если a делится на p.

L(a,p) = 1, если a - квадратичный вычет по модулю p.

L(a,p) = -1, если a не является квадратичным вычетом по модулю p.

L(a,p) можно рассчитать следующим образом:

L(a,p = a(p-1)/2 mod p

Или можно воспользоваться следующим алгоритмом:

1.Если a = 1, то L(a,p) = 1

2.Если a четно, то L( a,p) = L(a/2,p) * "2-1)/8

3.Если a нечетно (и Ф 1), то L(a,p)= L(p mod a, p)*(-1)(a-1)(p-1)/4

Этот метод также является эффективным способом определить, является ли a квадратичным вычетом по модулю p (для простого числа p).

С

29

имвол Якоби, J(a,n), представляет собой обобщение символа Лежандра на составные модули, он определяется для любого целого а и любого нечетного целого п. Функция удобна при проверке на простоту. Символ Як о-би является функцией на множестве полученных вычетов делителей п и может быть вычислен по различным формулам. Вот один из способов: Определение 1: J (а,п) определен, только если п нечетно. Определение 2: J(0,«) = 0. Определение 3: Если п - простое число, то символ Якоби J (а,п) = О, если а делится на п. Определение 4: Если п - простое число, то символ Якоби J(a,n) = 1, если а - квадратичный вычет по модулю п. Определение 5: Если п - простое число, то символ Якоби ](а,п) = -1, если а не является квадратичным выче­том по модулю п. Определение 6: Если п - составное число, то символ Якоби J(a,n) = J(a,p1)* ... * J(a,pm), где р1, ... , рт - это разложение п на простые сомножители.

Следующий алгоритм рекурсивно рассчитывает символ Якоби: Правило 1: J(l,n) = 1 Правило 2: J(a*b,n) = J(а,п)* J(b,n) Правило 3: J(2,n) =, если (n2-1) /8 нечетно, и -1 в противном случае Правило 4: J(а,п)= J((a mod n),n) Правило 5: J(a, b1*b2) = J(a, b1)* J(a, b2) Правило 6: Если наибольший общий делитель а и b = 1, а также а и b нечетны: Правило 6а: J(a,b)= J(b, а), если (a - 1)(b - l)/4 четно Правило 6b: J(a,b)= -J(b, а), если (а - 1)(b - 1)/4 нечетно

Если заранее известно, что n - простое число, вместо использования предыдущего алгоритма просто вычислите а((n-1)/2) mod n, в этом случае J(а,п) эквивалентен символу Лежандра.

Символ Якоби нельзя использовать для определения того, является ли а квадратичным вычетом по модулю п (если, конечно, п не является простым числом). Обратите внимание, что если J( а,п) = 1 и п - составное число, то утверждение, что а является квадратичным вычетом по модулю п, не обязательно будет истиной. Например: J(7,143) = J(7, l l)* J(7,13) = (-1)(-1) = 1 Однако не существует таких целых чисел х, что х2 = 7 (mod 143).

Если р и q - два простых числа, конгруэнтных 3 по модулю 4, то п = pq иногда называют целым числом Блюма. Если п - это целое число Блюма, у каждого квадратичного вычета ровно четыре квадратных корня, один из которых также является квадратом - это главный квадратный корень. Например, главный квадратный корень 139 mod 437 - это 24. Остальные три корня - это 185, 252 и 413.

Контрольные вопросы:

24. Как определяется символ Лежандра?

25. Что представляет из себя символ Якоби?

26. Что называют целым числом Блюма?

30

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №11

ГЕНЕРАТОРЫ

Если р - простое число, и g меньше, чем р, то g называется генератором по модулю р, если для каждого числа b от 1 до р-1 существует некоторое число а, что ga = b (mod p) [6].

Иными словами, g является примитивом по отношению к р. Например, если р = 11, то 2 - это генератор по модулю 11:

2*6 = 12=1 (mod 11) 2*1 = 2 = 2 (mod 11) 2*7 = 14 = 3 (mod 11) 2*2 = 4 = 4 (mod l l) 2*8 =16 = 5 (mod l l) 2*3 = 6 = 6 (mod 11) 2*9 = 18 = 7 (mod 11) 2*4 = 8 = 8 (mod l l) 2*10 = 20 = 9 (mod l l) 2*5 = 32 = 10 (mod 11)

Каждое число от 1 до 10 может быть представлено как 2a (mod p). Для р = 11 генераторами являются 2, 6, 7 и 8. Другие числа не являются генераторами. Например, генератором не является число 3, потому что не существует решения для 3a = 2 (mod 11)

В общем случае проверить, является ли данное число генератором, нелегко. Однако задача упрощается, е сли известно разложение на множители для р - 1. Пусть q1, q2, ... , qn - это различные простые множители р - 1. Чтобы проверить, является ли число g генератором по модулю р, вычислите g(p-1)/q mod p для всех значений q = q1 q2,..., qn.

Если это число равно 1 для некоторого q, то g не является генератором. Если для всех значений q рассчитан­ное значение не равно 1, то g - это генератор.

Например, пусть р = 11. Простые множители р - 1 = 10 - это 2 и 5. Для проверки того, является ли число 2 генератором, вычислим: 2(11-1)/5 (mod 11) = 4

2(11-1)/2 (mod 11) = 10

Н

31

и один из ответов не равен 1, поэтому 2 - это генератор. Проверим, является генератором ли число 3: 3(11-1)/5 (mod 11) = 9 3(11-1)/2 (mod 11) = 1 Следовательно, 3 - это не генератор.

При необходимости обнаружить генератор по модулю р просто случайно выбирайте число от 1 до р - 1 и проверяйте, не является ли оно генератором. Генераторов достаточно, поэтому один из них вы, скорее всего, найдете быстро.

Контрольные вопросы:

27. Что называют генератором по модулю р?

28. Как упростить задачу проверки: является ли данное число генератором?

29. Как обнаружить генератор по модулю p?

32

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №12

ДИОФАНТОВЫ УРАВНЕНИЯ

Диофантовыми называются уравнения вида

P(x₁, x₂, ..., x_n) = 0,

где P(x₁, ..., x_n) – многочлен с целыми коэффициентами.

Рассмотрим алгоритм нахождения решения линейного диофантового уравнения с двумя неизвестными вида a·x + b·y = c (далее для простоты будем опускать знаки умножения и писать прото ax + by = c) [5].

Теорема 1. Уравнение ax + by = c имеет решение в целых числах тогда и только тогда, когда c делится на НОД(a, b).

Теорема 2. Если пара (x₀, y₀) является решением уравнения ax + by = c, то все множество его решений (x, y) описывается формулой:

x = x₀ + kb,

y = y₀ – ka,

   где k Є Z. Очевидно, что если ax₀ + by₀ = c, то a(x₀ + kb) + b(y₀ – ka) = c для любого целого k.

   Для нахождения частичного решения (x₀, y₀) уравнения ax + by = c следует сначала найти решение (x’, y’) уравнения ax + by = d (d – наибольший общий делитель a и b) при помощи расширенного алгоритма Евклида, после чего умножить его на c / d. То есть

x₀ = x’ · c / d,

y₀ = y’ · c / d

Пример. Найти множество решений уравнения 5x + 3y = 7.

   1. Уравнение имеет решение, так как 7 делится на НОД(5, 3) = 1.

   2. Находим решение уравнения 5x’ + 3y’ = 1 при помощи расширенного алгоритма Евклида: (x’, y’) = (-1, 2).

   3. Находим решение (x₀, y₀) исходного диофантового уравнения:

x₀ = -1 · 7 / 1 = -7,

y₀ = 2 · 7 / 1 = 14

   Согласно теореме 2 множество решений исходного диофантового уравнения имеет вид:

(x, y) = (-7 + 3k, 14 – 5k)

33

Контрольные вопросы:

30. Какие уравнения называют диофантовыми?

31. В каком случае уравнение ax + by = c имеет решение в целых числах?

32. Каков алгоритм нахождения решения линейного диофантового уравнения с двумя неизвестными вида a·x + b·y = c?

34