
Частина 2
.pdf
“Курс вищої математики. Частина 2.”
Якщо побудувати в крапці А кривій нормаль, направлену у бік опуклості, то можна відкласти відрізок АС = R, де R – радіус кривизни кривої в точці А. Тогда крапка З(а, b) називається центром кривизни кривої в крапці А.
Круг радіусу R з центром в крапці З називається довкола кривизни.
Очевидно, що в крапці А кривизна кривої і кривизна кола рівні.
Можна показати, що координати центру кривизни можуть бути знайдені по формулах:
|
′ |
+ y |
′2 |
) |
|
|
1 + y |
′2 |
|
a = x − |
y (1 |
|
; |
b = y + |
|
; |
|||
|
y′′ |
|
|
y′′ |
|
||||
|
|
|
|
|
|
|
|
||
Визначення: Сукупність всіх центрів кривизни кривої лінії утворюють нову лінію, яка називається еволютою по відношенню до даної кривої. По відношенню до еволюти початкова крива називається евольвентою.
Приведені вище рівняння, що визначають координати центрів кривизни кривої визначають рівняння еволюти.
Властивості еволюти.
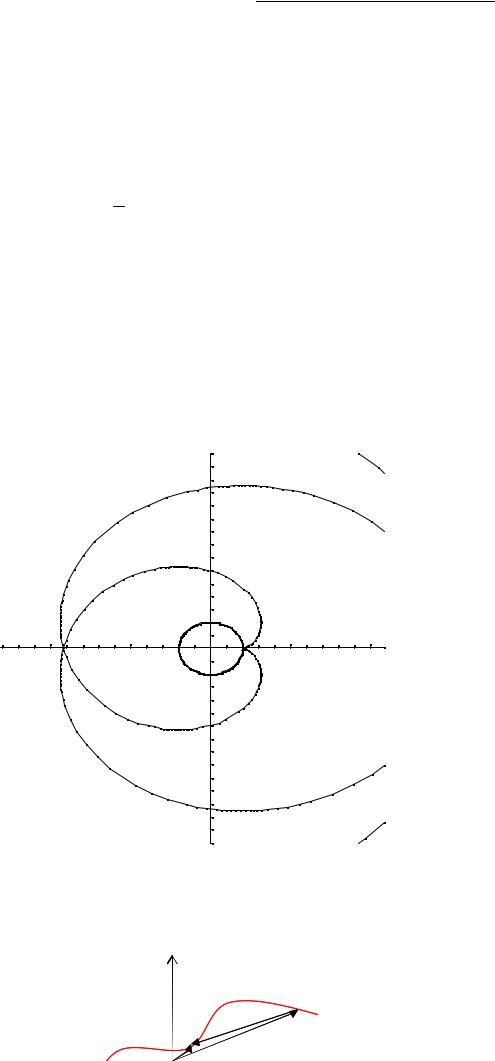
Теорема 1: Нормаль до даної кривої є дотичною до її еволюти.
Теорема 2: Модуль різниці радіусів кривизни в будь-яких точках кривої рівний модулю довжини відповідної еволюти.
С3
С2
С1
R1 R2 R3
M1
M’1 M2 M3
M’2
M’3
Треба відзначити, що який – або еволюті відповідає нескінченне число евольвент. Вказані вище властивості можна проілюструвати таким чином: якщо на еволюту натягнута нитка, то евольвента виходить як траєкторна лінія кінця нитки при її змотуванні або розмотуванні за умови, що нитка знаходиться в натягнутому стані.
41
“Курс вищої математики. Частина 2.”
Приклад: Знайти рівняння еволюти кривою, заданою рівняннями:
x = a(cost +t sin t)y = a(sin t −t cost)
x& = a(−sin t +sin t +t cost) = at costy& = a(cost −cost +t sin t) = at sin t
y′ = xy&& = tgt; 1+ ( y′)2 = sec2 t,
y′′ = |
d(tgt) |
= |
d(tgt) |
|
dt |
= sec |
2 |
t |
1 |
= |
sec3 t |
dx |
dt |
dx |
|
& |
at |
||||||
|
|
|
|
|
|
x |
|
Рівняння еволюти: |
|
|
Остаточно: |
p = a cost |
- це рівняння кола з центром на початку координат радіусу а. |
|
||
|
q = a sin t |
|
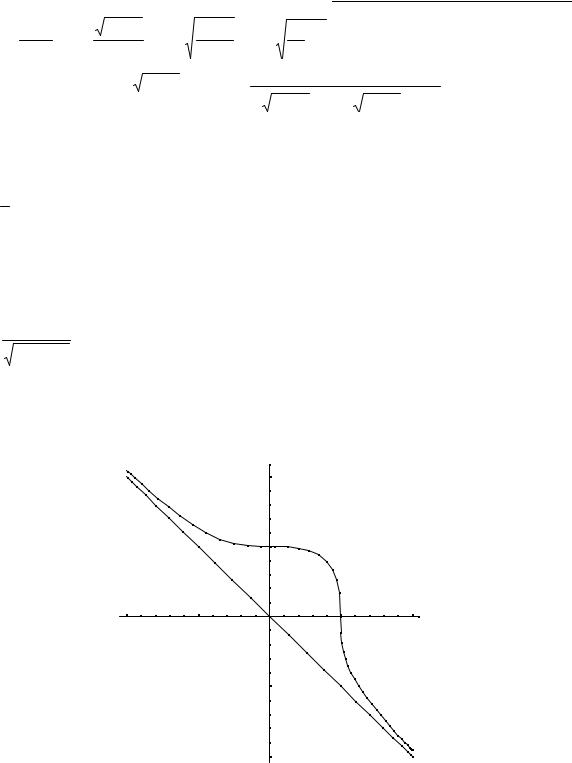
Початкова крива виходить свого роду розгорткою кола. Нижче приведені графіки початкової кривої і її еволюти.
|
|
15 |
|
|
|
10 |
|
|
|
5 |
|
-10 |
-5 |
5 |
10 |
|
|
-5 |
|
|
|
-10 |
|
|
|
-15 |
|
|
Кривизна просторової кривої. |
|
|
42

“Курс вищої математики. Частина 2.”
A(x, у, z)
B
r + ∆r |
r |
0 у
x
Для довільної крапки А, що знаходиться на просторовій кривій, координати можуть бути визначені як функції деякої довжини дуги S.
x = (S); |
у = (S); |
z = f(S); |
rr = rr(S) = ϕ(S)i + ψ(S) j + f (S)k ;
Приведене вище рівняння називають векторним рівнянням лінії в просторі.
Визначення: Лінія, яку опише в просторі змінний радіус, – вектор при зміні параметра S, називається годографом цього вектора.
r |
|
|
AB |
|
dr |
|
∆r |
|
|
∆r |
= |
|
|
|
тоді |
= lim |
- вектор, направлений по дотичній до кривій в крапці А(x, |
||
|
|
|
|||||||
∆S |
|
|
dS |
∆S |
|||||
|
|
AB |
∆S →0 |
|
|||||
|
|
|
|
|
|
|
|||
у, z).
Але оскільки, то ar = dSdr - одиничний вектор, направлений по дотичній.
|
|
r |
|
dx r |
|
dy |
|
r |
|
dz |
r |
||
Якщо прийняти, то a |
= |
|
i |
+ |
|
|
j |
+ |
|
k . |
|||
dS |
dS |
|
dS |
||||||||||
dx 2 |
dy |
2 |
|
dz |
2 |
=1 . |
|
||||||
Причому |
|
+ |
|
|
|
+ |
|
|
|||||
dS |
dS |
|
|
dS |
|
|
|
|
|||||
Розглянемо другу похідну
Визначення: Пряма, що має напрям вектора називається головною нормаллю до кривій. Її одиничний вектор позначається n .
dSda = K nr де До – кривизна кривої.
d 2 rr |
= |
nr |
; |
|
dS 2 |
R |
|||
|
|
Кривизна просторової кривої може бути знайдена по формулі:
K =  (rr′×rr′′)2
(rr′×rr′′)2
 [(rr′)2 ]3
[(rr′)2 ]3
43

“Курс вищої математики. Частина 2.”
Можливий і інший запис формули для кривизни просторової кривої (вона виходить з приведеної вище формули):
|
|
2 |
r |
|
2 |
|
2 |
r |
|
|
2 |
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
2 |
|
r |
|
d |
r |
|
x |
|
y |
|
z |
|
|||||||||||||
K = |
d |
|
|
= |
|
= |
d |
|
|
|
d |
|
|
|
d |
|
|
|
||||||
|
|
2 |
|
dS |
2 |
|
|
2 |
|
+ |
|
2 |
|
+ |
|
2 |
|
|||||||
|
dS |
|
|
|
|
|
dS |
|
|
|
dS |
|
|
|
dS |
|
|
|
||||||
Визначення: Вектор |
d 2 rr |
називається |
вектором кривизни. Величина ρ = |
1 |
|
dS 2 |
K |
||||
|
|
|
називається радіусом кривизни.
Про формули Френе.
Формулами Френе називаються співвідношення:
dar |
= |
nr |
; |
db |
= |
nr |
; |
dnr |
= − |
ar |
− |
b |
; |
|
dS |
R |
dS |
T |
dS |
R |
T |
||||||||
|
|
|
|
|
|
|
nr = b ×ar;
Остання формула отримана з двох перших.
У цих формулах: r
nr - одиничний вектор головної нормалі до кривій
b - одиничний вектор бинормали R – радіус кривизни кривої
Т – радіус кручення кривої.
Визначення: Площина, що проходить через дотичну і головну нормаль до кривій в крапці А називається дотичною площиною.
Визначення: Нормаль до кривій, перпендикулярна до дотичної площини, називається бинормалью. Її одиничний вектор- b .
rr
db |
|
1 |
|
db |
|
1 |
r |
|
= |
|
; |
|
= |
|
n; |
dS |
T |
dS |
T |
Величина T1 називається крученням кривої.
Нижче розглянемо декілька прикладів дослідження методами диференціального числення різних типів функцій.
Приклад: Методами диференціального числення досліджувати функцію y = 3 1− x3 і побудувати її графік.
1.Областю визначення даної функції є всі дійсні числа (-∞; ∞).
2.Функція є функцією загального вигляду в сенсі парності і непарності.
3.Точки перетину з координатними осями: з віссю Оу: x = 0; у = 1;
звіссю Ох: у = 0; x = 1;
4.Точки розриву і асимптоти: Вертикальних асимптот немає.
Похилі асимптоти: загальне рівняння у = kx + b;
44
“Курс вищої математики. Частина 2.”
k = lim |
f (x) |
3 |
1− x3 |
= lim 3 |
1 |
− x3 |
|
|
1 |
|
−1 = −1; |
|
|
|
|
|
|
|||
x |
= lim |
x |
|
x3 |
= lim |
3 |
|
|
|
|
|
|
|
|
||||||
x→∞ |
x→∞ |
x→∞ |
|
|
x→∞ |
x3 |
|
|
|
|
|
|
|
|
|
|||||
b = lim( f (x) − kx) = lim(3 |
1 − x3 + x) = lim |
3 |
|
|
|
(1 − x3 + x3 ) |
|
|
|
|
= 0; |
|||||||||
x→∞ |
|
|
x→∞ |
|
|
|
x←∞ |
|
− x |
3 |
2 |
3 |
1 |
− x |
3 |
+ x |
2 |
|
||
|
|
|
|
|
|
|
|
( 1 |
|
) − x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разом: у = -х – асимптота похилої.
5. Зростання і убування функції, точки екстремуму.
y′ = 13 (1− x3 )2 / 3 (−3x2 ). Видно, що у 0 при будь-якому х ≠ 0, отже, функція убуває на
всій області визначення і не має екстремумів. У точці х = 0 перша похідна функції рівна нулю, проте в цій крапці убування не змінялося на зростання, отже, в точці х = 0 функція швидше за все має перегин. Для знаходження точок перегину, знаходимо другу похідну функції.
y′′ = |
− 2x |
у′′ = 0 при х =0 і у′′ = ∞ при х = 1. |
3 |
(1 − x3 )5 |
|
Крапки (0,1) і (1,0) є точками перегину, оскільки у′′(1-h)< 0; у′′(1+h) >0; у′′(-h)> 0; у(h)<
′′0 для будь-якого h > 0.
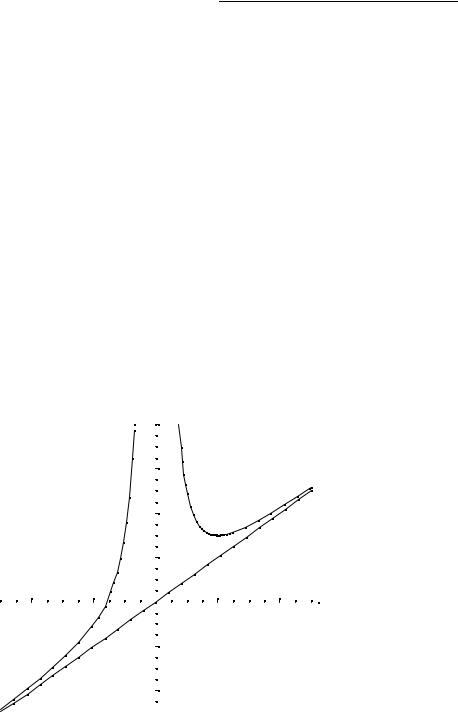
6. Побудуємо графік функції. |
|
|
|
|
|
2 |
|
|
|
1 |
|
-2 |
-1 |
1 |
2 |
|
|
-1 |
|
|
|
-2 |
|
|
Приклад: Досліджувати функцію y = |
|
x3 |
+ 4 |
і побудувати її графік. |
|
|
x2 |
|||
|
|
|
|
||
1. |
Областю визначення функції є всі значення х, окрім х = 0. |
||||
2. |
Функція є функцією загального вигляду в сенсі парності і непарності. |
||||
3. |
Точки перетину з координатними осями: з віссю Ох: у = 0; x = |
||||
|
з віссю Оу: x = 0; у – не існує. |
|
|
|
|
4. |
Точка х = 0 є точкою розриву, отже, пряма х = 0 є вертикальною асимптотою. |
||||
Похилі асимптоти шукаємо у вигляді: у = kx + b. |
|
||||
|
45 |
|
|
|
|
“Курс вищої математики. Частина 2.”
k = lim |
|
f (x) |
|
x3 + 4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
= lim |
|
|
|
= lim 1 + |
|
|
|
=1 |
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
x3 |
|
x3 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x→∞ |
x→∞ |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
+ |
4 |
|
|
|
|
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 = 0. |
|
|
|
|
||||||||
b = lim( f (x) − kx) = lim |
|
|
x |
|
− x = lim |
|
|
|
|
|
|||||||||||||||||||
|
|
x→∞ |
|
|
|
x→∞ |
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
|
|
|||||||||
Асимптота похилої у = х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. Знаходимо точки екстремуму функції. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y |
′ |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 − x3 ; |
у′ = 0 при х = 2, у′ = |
∞ при х = 0. |
|
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
у′ > 0 при х (-∞, 0) – функція зростає |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
у′ < 0 при х (0, 2) – функція убуває |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
у′ > 0 при х (2 ∞) – функція зростає. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Таким чином, крапка (2, 3) є точкою мінімуму. |
|
|
|||||||||||||||||||||||||||
|
|
|
Для визначення характеру опуклості/угнутості функції знаходимо другу |
||||||||||||||||||||||||||
похідну. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y′′ = |
|
> 0 при будь-якому х ≠ 0, отже, функція увігнута на всій області визначення. |
|||||||||||||||||||||||||||
x4 |
|||||||||||||||||||||||||||||
6. Побудуємо графік функції. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
-2 |
|
|
|
|
|
2 |
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад: Досліджувати функцію y = x(x −1)3 і побудувати її графік. |
|||||
1. |
Областю визначення даної функції є проміжок х (- ∞). |
|||||
2. |
У сенсі парності і непарності функція є функцією загального вигляду. |
|||||
3. |
Точки перетину з осями координат: з віссю Оу: x = 0, у = 0; |
|||||
4. |
Асимптоти кривої. |
|
з віссю Ох: у = 0, x = 0, x = 1. |
|||
|
|
|||||
Вертикальних асимптот немає. |
||||||
Спробуємо знайти похилі асимптоти у вигляді у = kx + b. |
||||||
k = lim |
f (x) |
= lim |
x(x −1) |
3 |
= ∞ - похилих асимптот не існує. |
|
x |
x |
|
||||
|
x→∞ |
x→∞ |
|
|
||
46

“Курс вищої математики. Частина 2.”
5. Знаходимо точки екстремуму.
y′ = [x(x3 −3x2 + 3x −1]′ = [x4 −3x3 + 3x2 − x]′ = 4x3 −9x2 + 6x −1
Для знаходження критичних крапок слід вирішити рівняння 4х3 – 9х2 +6х –1 = 0. Для цього розкладемо даний многочлен третього ступеня на множники. Підбором можна визначити, що одним з коріння цього рівняння є число х = 1. Тоді:
4x3 – 4x2 |
4x3 – 9x2 + 6x – 1 |
x - 1 |
||||||
|
|
4x2 – 5x + 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
- 5x2 + 6x |
||||||
|
- 5x2 + 5x |
|||||||
|
|
|
x - 1 |
|
|
|
||
x - 1 |
|
|
|
|||||
|
0 |
|
|
|||||
Тоді можна записати (х – 1)(4х2 – 5х + 1) = 0. Остаточно отримуємо дві критичні крапки: x = 1 і x = ј.
Примітка. Операції ділення многочленів можна було уникнути, якщо при знаходженні похідної скористатися формулою похідної твору:
y′ = [x(x −1)3 ]′ = (x −1)3 + 3x(x −1)2 = (x −1)2 (x −1 + 3x) = (x −1)2 (4x −1)
Знайдемо другу похідну функції: 12x2 – 18x + 6. Прирівнюючи до нуля, знаходимо: x = 1, x = Ѕ.
Систематизуємо отриману інформацію в таблиці:
|
|
(-∞ ; ј) |
1/4 |
( ј ; Ѕ) |
1/2 |
( Ѕ ; 1 ) |
1 |
(1 ; ∞) |
f(x) |
|
+ |
+ |
+ |
0 |
- |
0 |
+ |
f(x) |
|
- |
0 |
+ |
+ |
+ |
0 |
+ |
f(x) |
|
убуває |
min |
зростає |
пере |
зростає |
пере |
зростає |
|
|
вып.вниз |
|
вып.вниз |
гин |
вып.вверх |
гин |
вып. вниз |
6. |
Побудуємо графік функції. |
|
|
|
|
|
||
47

“Курс вищої математики. Частина 2.”
0.4
0.2
-0.5 |
0.5 |
1 |
1.5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
-0.2
-0.4
Інтегральне числення.
Первісна функція.
Визначення: Функція F(x) називається первісною функцією функції f(x) на відрізку [а, b], якщо в будь-якій точці цього відрізання вірна рівність:
F(x)= f(x).
Треба відзначити, що первісних для однієї і тієї ж функції може бути нескінченне багато. Вони відрізнятимуться один від одного на деяке постійне число.
F1(x)= F2(x)+ C.
Невизначений інтеграл.
Визначення: Невизначеним інтегралом функції f(x) називається сукупність первісних функцій, які визначені співвідношенням:
F(x)+ C.
Записують:
Умовою існування невизначеного інтеграла на деякому відрізку є безперервність функції на цьому відрізку.
Властивості:
1.(∫ f (x)dx)′ = (F(x) +C)′ = f (x);
2.d (∫ f (x)dx)= f (x)dx;
3.∫dF(x) = F(x) +C;
4.∫(u + v − w)dx = ∫udx + ∫vdx − ∫wdx; де u, v, w – деякі функції від х.
6. ∫C f (x)dx = C ∫ f (x)dx;
Приклад:
48
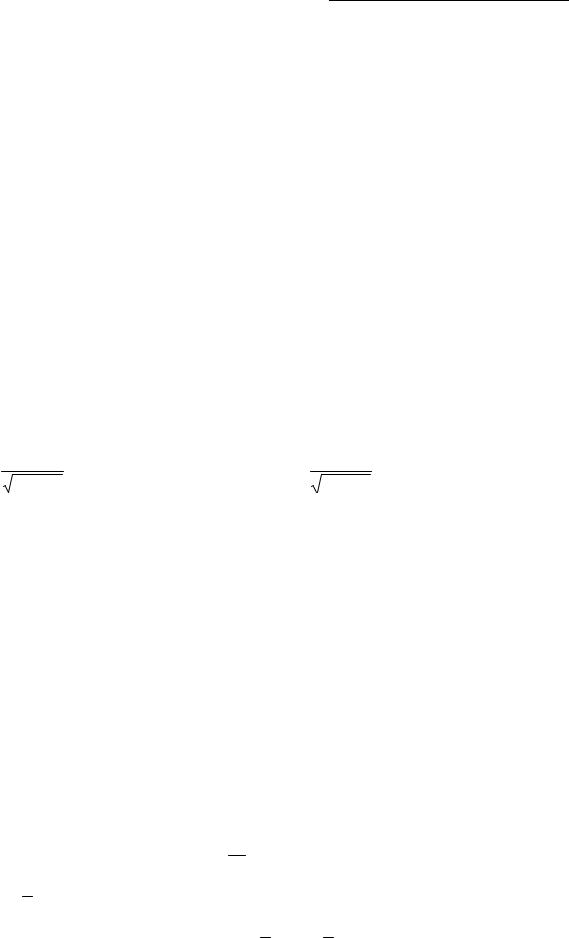
“Курс вищої математики. Частина 2.”
Знаходження значення невизначеного інтеграла пов'язане головним чином із знаходженням первісної функції. Для деяких функцій це достатньо складне завдання. Нижче будуть розглянуті способи знаходження невизначених інтегралів для основних класів функцій – раціональних, ірраціональних, тригонометричних, показових і ін.
Для зручності значення невизначених інтегралів більшості елементарних функцій зібрані в спеціальні таблиці інтегралів, які бувають іноді вельми об'ємними. У них включені різні найбільш комбінації функцій, що часто зустрічаються. Але більшість представлених в цих таблицях формул є следствиями один одного, тому нижче приведемо таблицю основних інтегралів, за допомогою якої можна набути значень невизначених інтегралів різних функцій.
|
Інтеграл |
|
|
|
Значення |
|
Інтеграл |
|
Значення |
|||||||||||||||||||||||||||||||||
1 |
∫tgxdx |
|
-ln cosx +C |
9 |
∫ex dx |
|
|
|
|
ex + C |
|
|
|
|||||||||||||||||||||||||||||
2 |
∫ctgxdx |
|
|
lnsinx+ C |
10 |
∫cos xdx |
|
sinx + C |
||||||||||||||||||||||||||||||||||
3 |
∫a x dx |
|
|
|
|
|
|
a x |
|
11 |
∫sin xdx |
|
-cosx + C |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4 |
∫ |
|
dx |
1 |
arctg |
x |
+C |
12 |
∫ |
1 |
|
|
|
dx |
|
|
tgx + C |
|||||||||||||||||||||||||
|
a2 + x2 |
|
|
|
a |
a |
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5 |
|
|
dx |
1 |
|
|
|
|
x + a |
|
|
|
13 |
|
1 |
|
|
|
|
|
-ctgx + C |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
∫ |
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
+C |
|
∫ |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x2 − a2 |
|
|
|
|
|
|
|
|
|
sin 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2a |
x − a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6 |
∫ |
|
dx |
ln |
|
|
|
|
|
|
|
|
|
|
|
14 |
∫ |
|
dx |
|
arcsin |
|
x |
+ C |
||||||||||||||||||
|
x2 ± a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 − x2 |
|
|
a |
||||||||||||||||||
7 |
∫ |
xαdx |
|
xα+1 |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
1 |
|
dx |
|
x |
|
|
π |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+C,α ≠ −1 |
|
|
|
|
|
ln |
tg |
|
|
|
+ |
|
|
|
|
|
+C |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∫cos x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
α +1 |
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
8 |
∫ |
dx |
|
|
|
|
|
|
|
|
|
ln |
|
x |
|
+ C |
16 |
∫ |
|
1 |
|
dx |
|
ln |
|
tg |
x |
|
+C |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
sin x |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методи інтеграції.
Розглянемо три основні методи інтеграції.
Безпосередня інтегрування.
Метод безпосередньої інтеграції заснований на припущенні про можливе значення первісної функції з подальшою перевіркою цього значення диференціюванням. Взагалі, відмітимо, що диференціювання є могутнім інструментом перевірки результатів інтеграції.
Розглянемо застосування цього методу на прикладі:
Потрібно знайти значення інтеграла ∫dxx . На основі відомої формули диференціювання
(ln x)′ = 1x можна зробити вивід, що шуканий інтеграл рівний, де З – деяке постійне
число. Однак, з іншого боку (ln(−x))′ = − 1x (−1) = 1x . Таким чином, остаточно можна зробити вивід:
49

“Курс вищої математики. Частина 2.”
∫dxx = ln x +C
Відмітимо, що на відміну від диференціювання, де для знаходження похідної використовувалися чіткі прийоми і методи, правила знаходження похідної, нарешті визначення похідної, для інтеграції такі методи недоступні. Якщо при знаходженні похідної ми користувалися, так би мовити, конструктивними методами, які, базуючись на певних правилах, приводили до результату, то при знаходженні первісною доводиться в основному спиратися на знання таблиць похідних і первісних.
Що стосується методу безпосередньої інтеграції, то він застосовний тільки для деяких вельми обмежених класів функцій. Функцій, для яких можна з ходу знайти первісну дуже мало. Тому в більшості випадків застосовуються способи, описані нижче.
Спосіб підстановки (заміни змінних).
Теорема: Якщо потрібно знайти інтеграл, але складно відшукати первісну, то за допомогою заміни x = (t) ϕі dx = (t)ϕ′dt виходить:
∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt
Доказ: Продиференціюємо пропоновану рівність: d ∫ f (x)dx = d (∫ f [ϕ(t)]ϕ′(t)dt)
По розглянутій вище властивості №2 невизначеного інтеграла: f(x)dx = f[(t)]ϕ(t)ϕ′dt
що з урахуванням введених позначень і є початковим припущенням. Теорема доведена.
Приклад. Знайти невизначений інтеграл ∫ sin x cos xdx .
sin x cos xdx .
Зробимо заміну t = sinx, dt = cosxdt. |
|
|
|
|
||||||||||||
∫ tdt = ∫t1/ 2 dt = |
2 t 3 / 2 |
+C = |
2 sin3 / 2 x +C. |
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
Приклад. |
|
|
|
|
|
|
|
dt |
|
|
|
|
|||
Заміна t = x2 +1; |
dt = 2xdx; |
dx = |
|
; Отримуємо: |
|
|||||||||||
2x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫t 3 / 2 |
dt |
= |
1 |
∫t 3 / 2 dt = |
1 |
|
2 |
t 5 / 2 |
+C = |
t 5 / 2 |
+C = |
(x2 +1)5 / 2 |
+C; |
|||
|
|
|
|
|
5 |
|||||||||||
2 |
2 |
|
2 |
5 |
|
5 |
|
|
|
|||||||
Нижче будуть розглянуті інші приклади застосування методу підстановки для різних типів функцій.
Інтегрування по частинах.
Спосіб заснований на відомій формулі похідної твору: (uv)′ = uv + vu
де u і v – деякі функції від х.
У диференціальній формі: d(uv)= udv + vdu
50
