13. Лекция № 13

13.1. Учет слабой заполненности матриц

В большинстве случаев матрица коэффициентов системы уравнений является слабозаполненной, то есть содержит большое число нулевых элементов, расположение которых произвольно. Такие матрицы называются слабозаполненными или разреженными [3].

Большинство взаимных проводимостей (элементов матрицы ) равно нулю, то есть слабозаполненна.

Учет слабой заполненности осуществляется алгоритмически очень просто при применении метода Зейделя (или простой итерации). Это легко сделать, используя информацию о топологической схеме сети, то есть о том, с какими узлами соединен узел k.

Наиболее простым и эффективным при применении метода Гаусса является способ нумерации узлов, при котором матрица присоединения узлов приводится к ленточной форме.

Матрицей в ленточной форме называют такую, у которой ненулевые элементы расположены в виде «ленты» вдоль главной диагонали матрицы (рис.13.1).

^а)

1 2 3 4 5 6 7 8

1

2

3

4

5

6

7

8

б)

Рис 13.1. Нумерация узлов приводящая матрицу присоединениния узлов к ленточной форме.

Номер узла тем больше, чем с большим количеством других узлов он соединен. Такой способ нумерации узлов приводит к существенному сокращению числа новых ненулевых элементов, возникающих в процессе исключения по Гауссу.

Существуют многочисленные способы нумерации узлов и учета слабой заполненности матрицы . Используя методы теории графов, можно с помощью специальных алгоритмов определять оптимальную с точки зрения экономии памяти и уменьшения числа операций нумерацию узлов.

Рассмотренные ниже способы эквивалентирования и разделения электрических систем на подсистемы особенно эффективны в сочетании с учетом слабой заполненности матриц.

13.2. Эквивалентирование при расчетах установившихся режимов

Пусть схема анализируемой электрической системы содержит n+1 узел. Диспетчеру надо проанализировать изменения режима при увеличении нагрузки в нескольких близко расположенных узлах. Это изменение нагрузки окажет влияние не на всю электрическую систему, а лишь на ее часть, допустим, из узлов, где . Целесообразно заменить всю электрическую систему из n+l узла на эквивалентную из узлов, содержащую только те узлы, для которых необходимо проанализировать изменения параметров режима. Затем надо рассчитать установившийся режим только эквивалентной системы из узлов.

Обычно при эквивалентировании предполагается, что в качестве активных элементов схема содержит только задающие токи; все ЭДС ветвей предполагаются предварительно замененными эквивалентными задающими токами.

Число независимых узлов исходной системы и порядок матрицы равны n. В эквивалентной системе содержится независимых узлов. При эквивалентировании исключается узел:

. (13.1)

Разобьем матрицу проводимостей и вектор-столбцы узловых напряжений и задающих токов на блоки, соответствующие эквивалентной системе и исключенной части. Запишем уравнение узловых напряжений - используя блочные матрицы и вектор-столбцы:

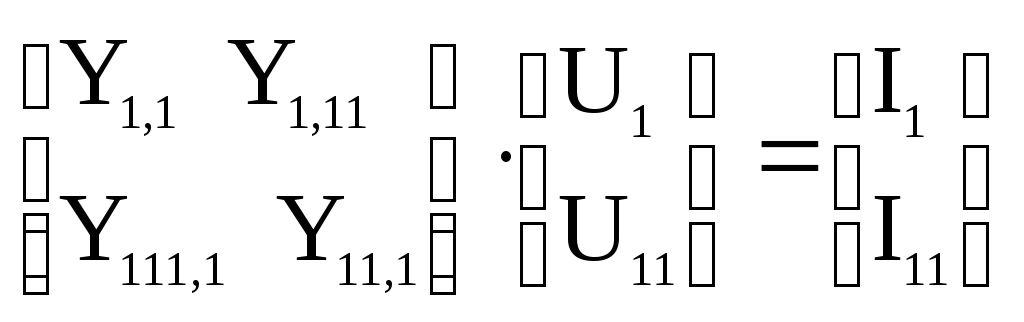. (13.2)

В этом уравнении Y - матрица собственных и взаимных проводимостей узлов эквивалентной системы; U_II , I_II - вектор-столбцы узловых напряжений и задающих токов эквивалентной системы; U₁ , I_I, Y_Ii включают узловые проводимости, напряжения и задающие токи исключаемых узлов; состоит из взаимных проводимостей узлов, уходящих в эквивалентную и исключаемую системы. Если записать (13.2) в виде двух матричных уравнений:

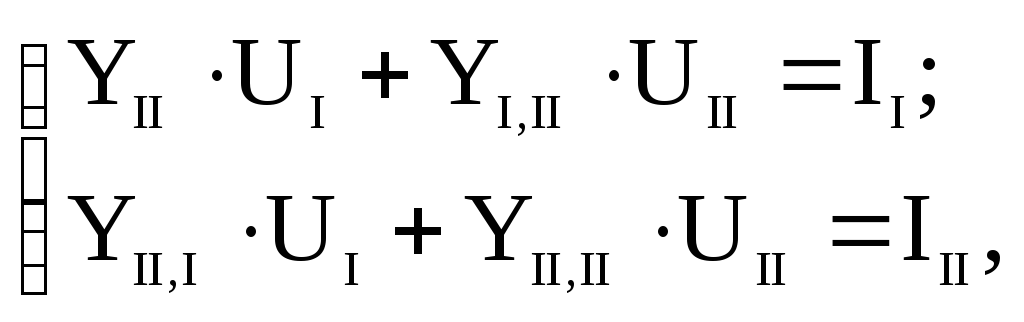(13.3)

то из первого уравнения можно выразить вектор-столбец напряжений исключаемых узлов через вектор-столбец напряжений эквивалентной системы:

. (13.3)

Если подставить последнее выражение во второе из уравнений (13.4), то получим уравнение узловых напряжении для эквивалентной системы:

. (13.5)

Перенесем первое слагаемое в правую часть этого уравнения и получим:

. (13.6)

Последнее перепишем в матричном виде:

. (13.7)

Таким образом, матрица узловых проводимостей и вектор-столбец задающих токов эквивалентной системы определяются следующими выражениями:

. (13.8)

. (13.9)

Последние слагаемые правой части выражений (13.8) и (13.9) отражают влияние исключенной части на напряжения узлов эквивалентной системы.

Более сложные способы эквивалентирования необходимо использовать для того, чтобы добиться совпадения при расчете эквивалентной и исходной систем не только напряжений, но и потерь мощности. Такие способы эквивалентирования всегда приводят к некоторой ошибке в определении потерь мощности и недостаточно разработаны для их практического применения при расчетах установившихся режимов. Особо важными и более сложными являются вопросы эквивалентирования электрических систем при расчетах переходных процессов.

13.3. Разделение на подсистемы и разделение уравнений

Разделение на подсистемы эффективно используется при расчетах установившихся режимов сложных электрических систем. Идея такого разделения состоит в том, чтобы рассчитать режим системы по частям.

При разделении на подсистемы определяются напряжения всех узлов электрической системы. Эффективность разделения на подсистемы состоит в том, что для каждой подсистемы решается меньшее количество уравнений с меньшим числом неизвестных, чем без такого разделения. Именно поэтому достигается экономия оперативной памяти ЭВМ. Такой путь позволяет увеличить объем рассчитываемых электрических систем и в ряде случаев уменьшить время расчета.

Разделение на подсистемы эффективно и при использовании итерационных методов. При разделении на подсистемы отдельно рассчитывается режим в каждой подсистеме.

Разделение на подсистемы и эквивалентирование фактически соответствуют записи матрицы в блочной форме, то есть разделению ее на блоки или подматрицы. Расчет режима при этом требует операций лишь с этими подматрицами. Различие между эквивалентированием и разделением на подсистемы в том, что разделение осуществляется так, что большинство подматриц состоит из нулей. Например, разделение на подсистемы целесообразно осуществить так, чтобы подматрица в (13.2) состояла только из нулей. В этом случае выражения (13.3) существенно упрощаются и можно независимо рассчитывать подсистемы I и II. Такое разделение возможно лишь в частном случае, когда две подсистемы не связаны друг с другом, но питаются от одного балансирующего узла. В более сложных случаях подсистемы связаны друг с другом через граничные ветви или узлы.

При разделении на подсистемы сети на (рис.13.2, а) матрица присоединения сети приводится к блочно-диагональной форме. Матрицей в блочно-диагональной форме называют такую, которая состоит из матриц-клеток (или блоков), расположенных по диагонали. Разделим схему соединения на три изолированные подсистемы (рис.13.2, б). Для этого разделим схему по узлу 12. Этот узел называется граничным. Пронумеруем узлы первой подсистемы в произвольном порядке (кроме граничного узла), затем узлы второй и третьей подсистем. Граничные узлы нумеруются в последнюю очередь. На (рис.13.2, в) приведена матрица присоединения узлов в блочно-диагональной форме. Здесь ненулевые элементы матрицы присоединения сгруппированы в отдельные квадратные матрицы-клетки (блоки), расположенные вдоль диагонали. Справа и снизу (то есть в последнем клеточном столбце и последней клеточной строке) они окаймляются ненулевыми элементами, не вошедшими в эти клетки (для схемы рис.13.2, а это элементы, соответствующие связям узла 12 со всеми остальными узлами).

Рис 13.2. Разбивка на подсистемы, приводящая матрицу узлов к блочно диагональной форме.

Решение системы уравнений с такой матрицей можно свести к независимому решению подсистем, которым соответствуют матрицы-клетки, расположенные вдоль главной диагонали, и решению некоторой линейной системы уравнений для узлов, не вошедших в эти системы (для узла 12 рис.13.2, а). Эта система уравнений называется системой границы и получается после исключения всех; переменных подсистем из уравнений этих узлов. Такой способ нумерации узлов в литературе иногда называют разбивкой на естественные и искусственные подсистемы [3].